Stationary points - Solution

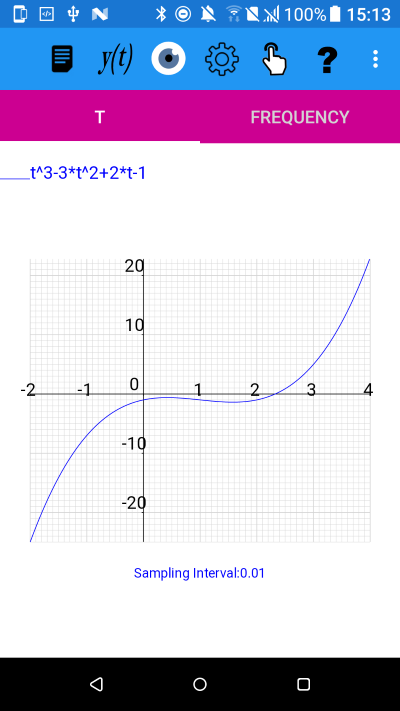
We select any continuous function e.g. t^3-3t^2+2*t-1 which we have plotted below, with -2<=t<4, using plotXpose.

t^3-3t^2+2*t-1

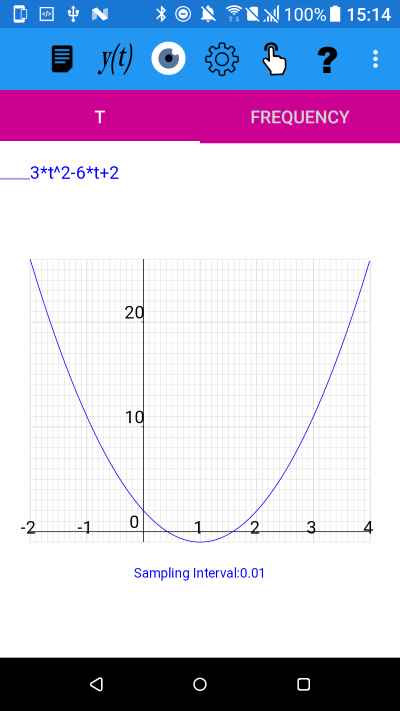
Differentiating z= t^3-3t^2+2*t-1 (using the rules of differentiation) we get :

dz/dt= 3*t^2-6*t+2

and we can now plot that derivative function using plotXpose

3t^2-6t+2

Using Mode -> Zero finding and changing the accuracy to 10 significant figures we tap near each of the two zeros of this derivative function.

Solving 3*t^2-6*t+2=0: Success. The Newton-Raphson method has converged to the value
(0.4226497308,0.0000000000E+000).
The sequence of values found was
( n, t , y(t))
(0, 0.15686275065, 1.13264126373E+000)
(1, 0.38075695542, 1.50385844788E-001)
(2, 0.42123267442, 4.91485148547E-003)
(3, 0.42264799605, 6.00940594353E-006)
(4, 0.42264973081, 9.02788954704E-012)
(5, 0.42264973081, 4.44089209850E-016)
(6, 0.42264973081, 0.00000000000E+000)

At this point, where t is approx 0.4226497308, the plotted derivative is going from positive to negative therefore represents a maximum of the original function.

Solving 3*t^2-6*t+2=0: Success. The Newton-Raphson method has converged to the value
(1.577350269,1.7763568394E-015).
The sequence of values found was
( n, t , y(t))
(0, 1.7058823109, 4.94809510386E-001)
(1, 1.5890522806, 4.09477679041E-002)
(2, 1.5774665043, 4.02690641170E-004)
(3, 1.5773502809, 4.05236200152E-008)
(4, 1.5773502692, -1.77635683940E-015)
(5, 1.5773502692, 8.88178419700E-016)
(6, 1.5773502692, 1.77635683940E-015)

At this point, where t is approx 1.577350269, the plotted derivative is going from negative to positive therefore represents a minimum of the original function.

plotXpose app is available on Google Play

Google Play and the Google Play logo are trademarks of Google LLC.
Versions will shortly be available for iOS and Windows.

plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.