Even sums can be odd! - Solution
Graphs of Even Functions and their Integrals with t0=0
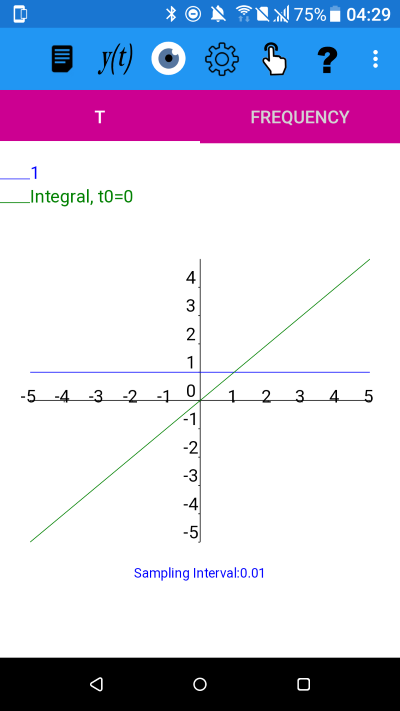
y=1
From the plot it appears that the integral is an odd function because if the integral graph is reflected in the y axis it results in an upside down version of itself (i.e. a reflection in the t-axis of the original plot).
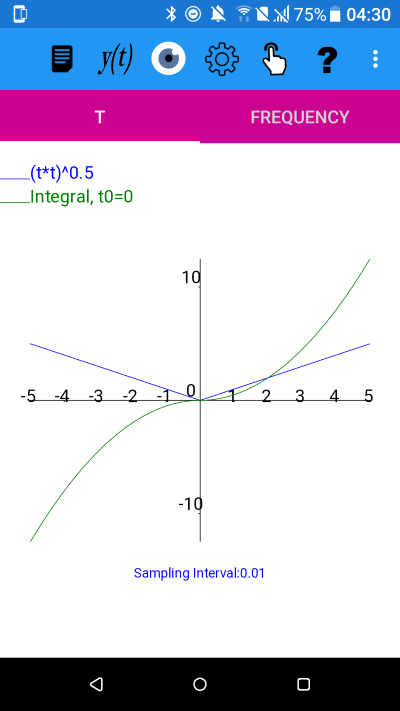
y=|t| using |t|=(t*t)^0.5
From the plot it appears that the integral is an odd function because if the integral graph is reflected in the y axis it results in an upside down version of itself (i.e. a reflection in the t-axis of the original plot).
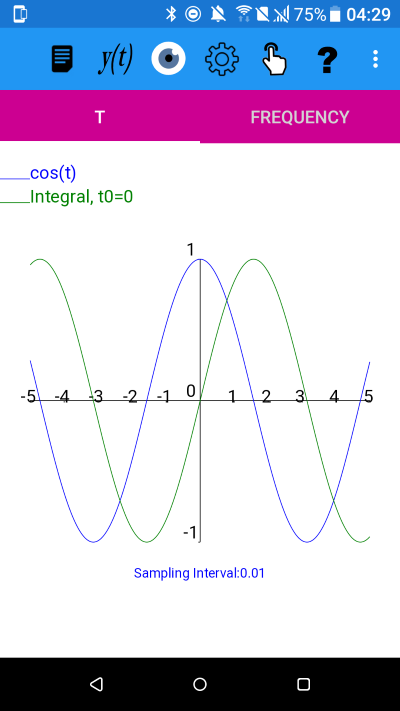
y=cos(t)
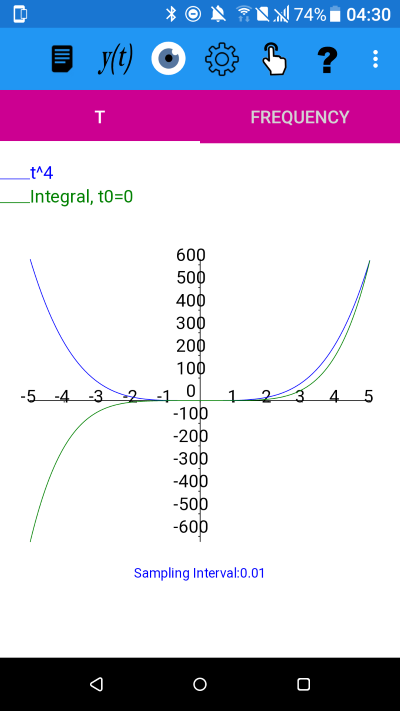
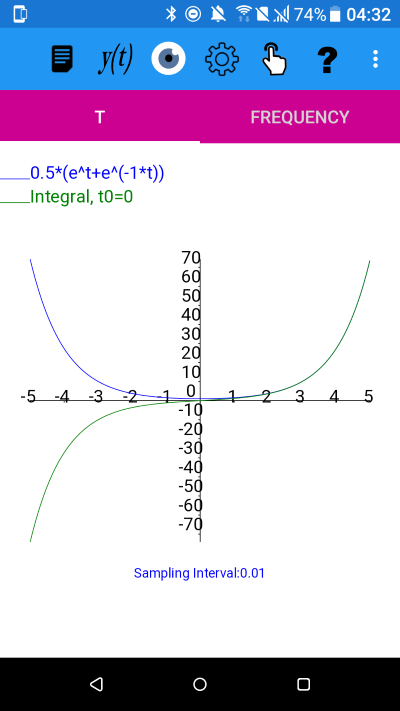
From the plot it appears that the integral is an odd function.
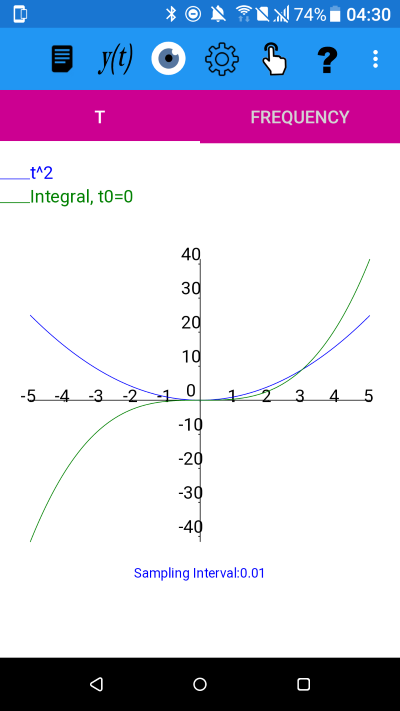
y=t^2
y=t^4
y=cosh(t) using cosh(t)=0.5*(e^t+e^(-1*t))
The Maclaurin series for a general function, f(t), defined around t=0 and with all its derivatives defined at t=0 is given by:
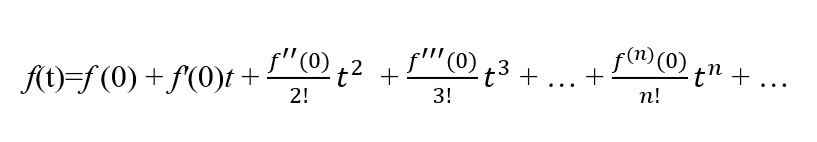
If a function is even then it will only have even powers of t in its Maclaurin series, i.e. f'(0) and f'''(0) and f(n)(0) for n odd, must all be 0.
So, for an even function the Maclaurin series is:
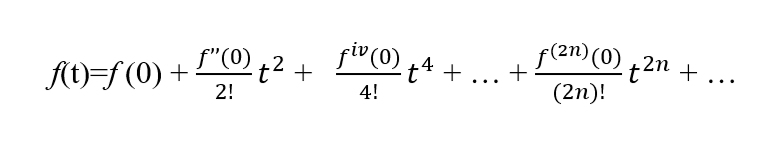
Integrating above we get
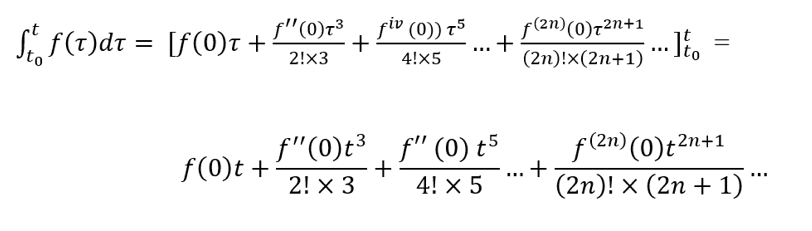
Providing t0=0.
As all the terms in the above are even powers of t then the integral is even, providing t0=0. For non-zero t0=0, no such conclusion can be made as the lower bound of the integration can result in a non-zero constant term, meaning that the integral is no longer even.
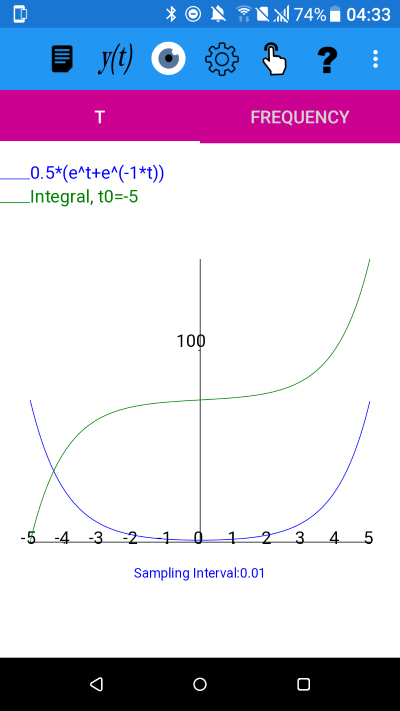
An example of the integral where t0 is non zero is given below.
y=cosh(t) using cosh(t)=0.5*(e^t+e^(-1*t)) and integral with t0=-5
The integral is not an odd function in this case.
plotXpose app is available on Google Play 
Google Play and the Google Play logo are trademarks of Google LLC.
Versions will shortly be available for iOS and Windows.
Google Play and the Google Play logo are trademarks of Google LLC.
Versions will shortly be available for iOS and Windows.
plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.