Converging sequence - Solution
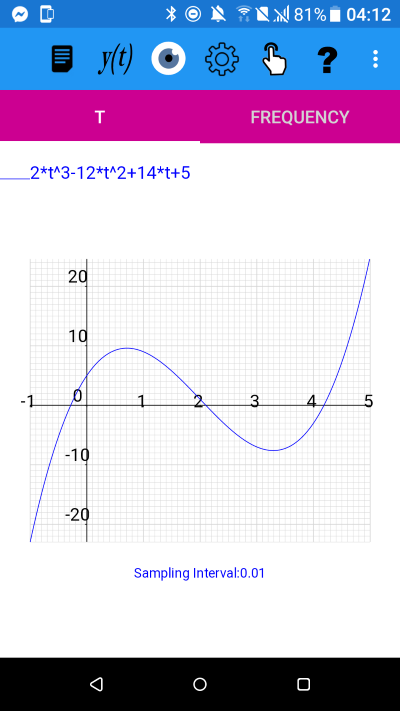
Plot of
y(t)=2*t^3-12*t^2+14*t+5
We have used the view menu to switch off the derivative display and display a grid, and used the Settings menu to change the t-axis limits to -1 to 5
Numerically solve 2*t^3-12*t^2+14*t+5 =0 using the Bisection method
Tap on the Mode icon and then the submenu ⋮ and select Zero Find. Change the radio to 'Bisection Method' the 'No. of s.f.' to 14 and the No. of iterations to 100. Example result below.
Solving 2*t^3-12*t^2+14*t+5=0: Success. The Bisection method has converged to the value (2.1002012096889,1.06581410364015E-014).
The sequence of values found was
( n, t , y(t))
(0, 1.26143789291382, 7.579888237905269E+000)
(1, 3.08496737480164, -7.295325934282026E+000)
(2, 2.17320263385773, -7.216344741674874E-001)
(3, 1.71732026338577, 3.781620715492245E+000)
(4, 1.94526144862175, 1.547057486553449E+000)
(5, 2.05923204123974, 4.080952111014113E-001)
(6, 2.11621733754873, -1.590340036264806E-001)
(7, 2.08772468939424, 1.241032980041723E-001)
(8, 2.10197101347148, -1.758952765572985E-002)
(9, 2.09484785143286, 5.322801001449307E-002)
(10, 2.09840943245217, 1.781175132050805E-002)
(11, 2.10019022296183, 1.092054840512446E-004)
(12, 2.10108061821666, -8.740641908374869E-003)
(13, 2.10063542058924, -4.315837888363205E-003)
(14, 2.10041282177554, -2.103346055015720E-003)
(15, 2.10030152236868, -9.970777404220144E-004)
(16, 2.10024587266525, -4.439379908802721E-004)
(17, 2.10021804781354, -1.673667189550088E-004)
(18, 2.10020413538768, -2.908073382457133E-005)
(19, 2.10019717917476, 4.006234601661163E-005)
(20, 2.10020065728122, 5.490798827167964E-006)
(21, 2.10020239633445, -1.179496931058566E-005)
(22, 2.10020152680784, -3.152085696456197E-006)
(23, 2.10020109204453, 1.169356451669046E-006)
(24, 2.10020130942618, -9.913646437098578E-007)
(25, 2.10020120073536, 8.899588976873929E-008)
(26, 2.10020125508077, -4.511843769705592E-007)
(27, 2.10020122790806, -1.810942436009100E-007)
(28, 2.10020121432171, -4.604916981065799E-008)
(29, 2.10020120752853, 2.147336175539749E-008)
(30, 2.10020121092512, -1.228790580398709E-008)
(31, 2.10020120922683, 4.592731528418881E-009)
(32, 2.10020121007597, -3.847588914140943E-009)
(33, 2.1002012096514, 3.725695307821297E-010)
(34, 2.10020120986369, -1.737511468036246E-009)
(35, 2.10020120975754, -6.824620868428610E-010)
(36, 2.10020120970447, -1.549551598145627E-010)
(37, 2.10020120967794, 1.088089618406229E-010)
(38, 2.1002012096912, -2.307132263013045E-011)
(39, 2.10020120968457, 4.287414867576445E-011)
(40, 2.10020120968789, 9.901413022816996E-012)
(41, 2.10020120968955, -6.586731160496129E-012)
(42, 2.10020120968872, 1.655564574321033E-012)
(43, 2.10020120968913, -2.454925152051146E-012)
(44, 2.10020120968892, -3.907985046680551E-013)
(45, 2.10020120968882, 6.252776074688882E-013)
(46, 2.10020120968887, 1.172395514004165E-013)
(47, 2.1002012096889, -1.421085471520200E-013)
(48, 2.10020120968888, -1.421085471520200E-014)
(49, 2.10020120968888, 5.329070518200751E-014)
(50, 2.10020120968888, 1.065814103640150E-014)
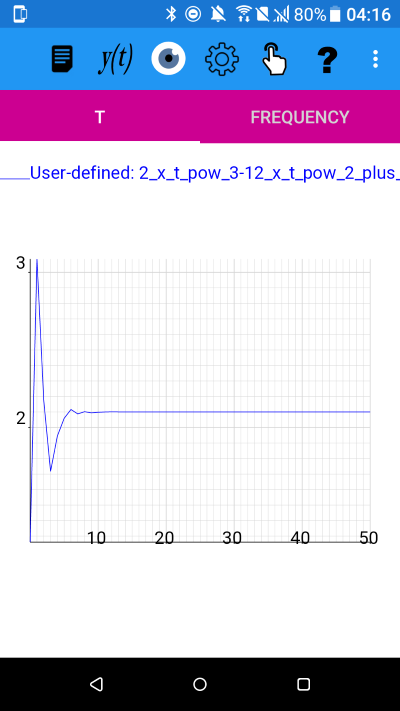
Tap on the File menu and then tap 'Save Zero Find Sequence'. Tap Open and read in the values as a new function. See result below.
From the plot of the zero-find sequence we can see that the values initially oscillate and then gradually approach the value of 2.1002012096889 which is a zero of 2*t^3-12*t^2+14*t+5 expressed to 14 s.f.
plotXpose app is available on Google Play 
Google Play and the Google Play logo are trademarks of Google LLC.
Versions will shortly be available for iOS and Windows.
Google Play and the Google Play logo are trademarks of Google LLC.
Versions will shortly be available for iOS and Windows.
plotXpose app is a companion to the book Mathematics for Electrical Engineering and Computing by Mary Attenborough, published by Newnes, 2003.